R-spatial beyond sf

posts
rstats
Author
Affiliation

Josiah Parry

Esri

Published

September 8, 2023

sf has transformed the R ecosystem and helped pave the way for wider adoption of geospatial workflows by R users. The R-spatial ecosystem, however, is much bigger than just sf. There are lower level packages such as geos, wk, and s2 that provide access to geometries and algorithms outside of the context of sf. These packages are often more performant than sf but require a different frame of mind when using them.

The goal of this post is to demystify the way in which sf represents geometries and explain how other geometry libraries can be used alongside typical sf workflows.

Understanding sf

Most R users that do geospatial analysis are familiar with sf and understand spatial workflows in that context only. Many users of sf view it as this magical data frame that lets you do spatial analysis—and that is exactly how it feels! This means that sf has done a great job in making spatial analysis feel a lot easier for the vast majority of R users.

Note

Read more about sf in Spatial Data Science

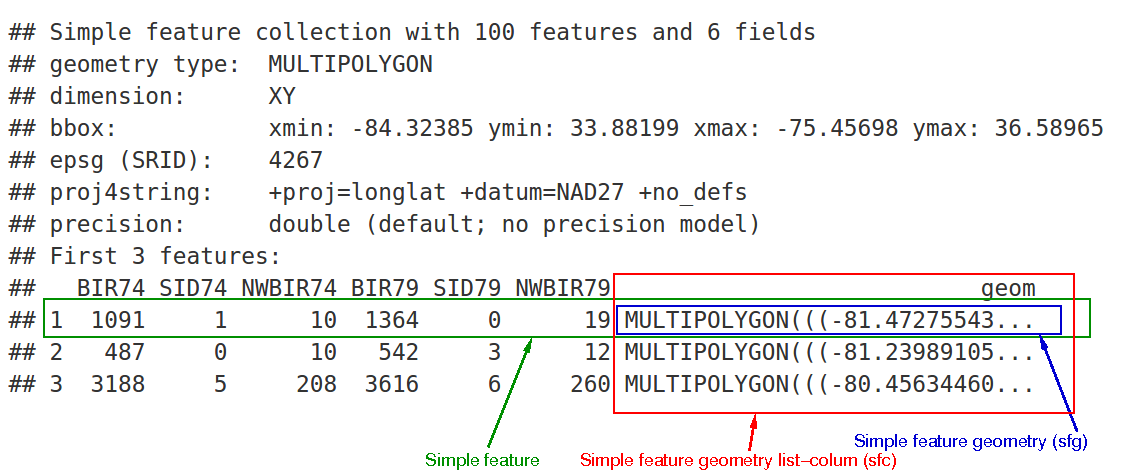
But it is good to understand sf in a more fundamental way. sf is named after the Simple Feature Access Standard. Simple features are an agreed upon way to represent “geometric primitives”—things like Points, LineStrings, Polygons, and their Multi- types. The sf package builds a hierarchy off of these. We have sfg, sfc, and sf objects.

sfg objects

At the core is the sfg class which is the representation of a simple feature geometry. sfg class objects are representations of a simple feature. They are a single geometry at a time. We can think of them as a scalar value (even though R does not have the concept of a scalar).

library(sf)
#> Linking to GEOS 3.11.1, GDAL 3.6.4, PROJ 9.1.1; sf_use_s2() is TRUE

# create a point
pnt <- st_point(c(0, 10))

# create a line
ln <- st_linestring(matrix(c(0, 1, 0, 0), ncol = 2))

class(pnt)
#> [1] "XY"    "POINT" "sfg"
class(ln)
#> [1] "XY"         "LINESTRING" "sfg"

Each scalar value can be used independently which is useful in itself.

st_length(ln)
#> [1] 1

sfg objects are very simple objects constructed of numeric vectors, matrices, and lists of matrices. They also have no sense of a coordinate reference system (CRS). More often than not, though, we want to have a vector of geometries—one for each element in a dataset, for example. In sf, a vector of geometries is stored in an sfc object.

sfc objects

sfc is short for simple feature column. You might think that you could create a vector of geometries by combining them using c() but that would be wrong

c(pnt, pnt)
#> MULTIPOINT ((0 10), (0 10))
c(pnt, ln)
#> GEOMETRYCOLLECTION (POINT (0 10), LINESTRING (0 0, 1 0))

sfg objects behave like scalars so combining them creates either a Multi- type of the sfg or a geometry collection (another type of simple feature).

To create a vector of geometries you must use st_sfc(). st_sfc() is the construct for creating a “simple feature geometry list column.” It lets you also set a number of attributes that are associated with the vector.

st_sfc(pnt, pnt)
#> Geometry set for 2 features 
#> Geometry type: POINT
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 10 xmax: 0 ymax: 10
#> CRS:           NA
#> POINT (0 10)
#> POINT (0 10)

Each sfc object contains attributes such as a CRS (optional), bounding box, and precision.

c(
  st_sfc(pnt, pnt), 
  st_sfc(pnt),
  st_sfc(ln)
)
#> Geometry set for 4 features 
#> Geometry type: GEOMETRY
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 1 ymax: 10
#> CRS:           NA
#> POINT (0 10)
#> POINT (0 10)
#> POINT (0 10)
#> LINESTRING (0 0, 1 0)

Under the hood, this is just a list of sfg objects. Remember, it’s not magic!

unclass(st_sfc(pnt, pnt))
#> [[1]]
#> POINT (0 10)
#> 
#> [[2]]
#> POINT (0 10)
#> 
#> attr(,"precision")
#> [1] 0
#> attr(,"bbox")
#> xmin ymin xmax ymax 
#>    0   10    0   10 
#> attr(,"crs")
#> Coordinate Reference System: NA
#> attr(,"n_empty")
#> [1] 0

Since sfc objects are vectors, they can be included as a column in a data frame.

df <- data.frame(
  geo = st_sfc(pnt, pnt)
)

df
#>       geometry
#> 1 POINT (0 10)
#> 2 POINT (0 10)

class(df)
#> [1] "data.frame"

Geometry and data.frames

Having geometry included in a data frame was a huge win for the R community because this means that attributes can be included along with geometries. Further, geometries in a data frame means that they are dplyr compatible.

For example we can create a vector of points from the x and y columns from the diamonds dataset in ggplot2.

data(diamonds, package = "ggplot2")

1pnts <- purrr::map2(
  diamonds$x, 
  diamonds$y, 
2  function(.x, .y) st_point(c(.x, .y))
) |> 
3  st_sfc()
1
We iterate over both the x and y columns in the diamonds dataset returning a list
2
Each value of x and y are accessed through the placeholder .x and .y based on their position in the map2() function. st_point() takes a length 2 numeric vector and returns a single sfg POINT object.
3
We pass the list of sfg objects to create an sfc

We can included this in a data frame

library(dplyr, warn.conflicts = FALSE)

dmnd <- diamonds |> 
  select(price, clarity) |> 
  bind_cols(geometry = pnts)

head(dmnd)
#> # A tibble: 6 × 3
#>   price clarity    geometry
#>   <int> <ord>       <POINT>
#> 1   326 SI2     (3.95 3.98)
#> 2   326 SI1     (3.89 3.84)
#> 3   327 VS1     (4.05 4.07)
#> 4   334 VS2      (4.2 4.23)
#> 5   335 SI2     (4.34 4.35)
#> 6   336 VVS2    (3.94 3.96)

Now we have a tibble with price, clarity, and geometry! Huge win! What if we wanted to calculate the average price by clarity and keep the geometries?

dmnd |> 
  group_by(clarity) |> 
  summarise(avg_price = mean(price))
#> # A tibble: 8 × 2
#>   clarity avg_price
#>   <ord>       <dbl>
#> 1 I1          3924.
#> 2 SI2         5063.
#> 3 SI1         3996.
#> 4 VS2         3925.
#> 5 VS1         3839.
#> 6 VVS2        3284.
#> 7 VVS1        2523.
#> 8 IF          2865.

Unfortunately, we lose the geometry just like we would for any other column that wasn’t included in the summarise() call. To keep it, we would need to perform an operation on the geometry itself.

dmnd |> 
  group_by(clarity) |> 
  summarise(
    avg_price = mean(price),
    geometry = st_union(geometry)
  )
#> # A tibble: 8 × 3
#>   clarity avg_price                                                     geometry
#>   <ord>       <dbl>                                                 <MULTIPOINT>
#> 1 I1          3924. ((4.33 4.29), (4.33 4.36), (4.36 4.33), (4.38 4.42), (4.39 …
#> 2 SI2         5063. ((0 0), (0 6.62), (3.79 3.75), (3.84 3.82), (3.87 3.85), (3…
#> 3 SI1         3996. ((3.88 3.84), (3.89 3.84), (3.9 3.85), (3.93 3.96), (3.95 3…
#> 4 VS2         3925. ((0 0), (3.73 3.68), (3.73 3.71), (3.74 3.71), (3.76 3.73),…
#> 5 VS1         3839. ((0 0), (3.83 3.85), (3.84 3.87), (3.86 3.89), (3.88 3.9), …
#> 6 VVS2        3284. ((3.83 3.86), (3.85 3.89), (3.85 3.9), (3.85 3.91), (3.86 3…
#> 7 VVS1        2523. ((0 0), (3.83 3.85), (3.87 3.9), (3.88 3.95), (3.88 3.99), …
#> 8 IF          2865. ((3.86 3.88), (3.89 3.9), (3.91 3.95), (3.92 3.94), (3.93 3…

Wouldn’t it be nice if the geometry knew to do that? Well, that is exactly what sf objects are.

sf objects

sf objects are just data frames with a geometry column that is sticky and smart. We can create an sf object if an sfc column is present in a data frame by using st_as_sf().

dmnd_sf <- st_as_sf(dmnd)

Doing this creates an object of class sf. The two things that make an sf object so special are the class sf and the attribute sf_column.

1attr(dmnd_sf, "sf_column")
#> [1] "geometry"
1
attr() lets us access a single attribute by name This attribute tells us which column is the geometry. Because we have this sf can implement its own methods for common functions like select(), mutate(), aggregate(), group_by(), etc which always keep the attr(x, "sf_column") attached to the data frame. Having the class and attribute allow methods like summarise() to be written for the class itself and handle the things like unioning geometry for us. 
dmnd_sf |> 
  group_by(clarity) |> 
  summarise(avg_price = mean(price))
#> Simple feature collection with 8 features and 2 fields
#> Geometry type: MULTIPOINT
#> Dimension:     XY
#> Bounding box:  xmin: 0 ymin: 0 xmax: 10.74 ymax: 58.9
#> CRS:           NA
#> # A tibble: 8 × 3
#>   clarity avg_price                                                     geometry
#>   <ord>       <dbl>                                                 <MULTIPOINT>
#> 1 I1          3924. ((4.33 4.29), (4.33 4.36), (4.36 4.33), (4.38 4.42), (4.39 …
#> 2 SI2         5063. ((0 0), (0 6.62), (3.79 3.75), (3.84 3.82), (3.87 3.85), (3…
#> 3 SI1         3996. ((3.88 3.84), (3.89 3.84), (3.9 3.85), (3.93 3.96), (3.95 3…
#> 4 VS2         3925. ((0 0), (3.73 3.68), (3.73 3.71), (3.74 3.71), (3.76 3.73),…
#> 5 VS1         3839. ((0 0), (3.83 3.85), (3.84 3.87), (3.86 3.89), (3.88 3.9), …
#> 6 VVS2        3284. ((3.83 3.86), (3.85 3.89), (3.85 3.9), (3.85 3.91), (3.86 3…
#> 7 VVS1        2523. ((0 0), (3.83 3.85), (3.87 3.9), (3.88 3.95), (3.88 3.99), …
#> 8 IF          2865. ((3.86 3.88), (3.89 3.9), (3.91 3.95), (3.92 3.94), (3.93 3…

Note that this is just like what we wrote earlier except that we didn’t have to handle the geometry column manually. If we compare these two approaches and ignore attribute difference like sf_column and class we can see that they are identical.

x <- dmnd |> 
  group_by(clarity) |> 
  summarise(
    avg_price = mean(price),
    geometry = st_union(geometry)
  )

y <- dmnd_sf |> 
  group_by(clarity) |> 
  summarise(avg_price = mean(price))

1all.equal(x, y, check.attributes = FALSE)
#> [1] TRUE
1
We ignore attributes because they will be different because the classes are different.

Other geometry vectors

Knowing how sf works can be helpful for understanding how we can ease our reliance on it for all geospatial operations. Instead of thinking of the entire sf data frame as the thing that handles all geometry operations we now know that it is the sfc geometry column.

In R there are different ways of representing geometry besides sfc vectors. The packages s2, geos, wk, and rsgeo all provide different vectors of geometries that can be used.

These libraries are very handy for doing geometric operations. Each of these packages tend to be better at one thing than another, and each have their place. You might find big speed improvements if you opt to use one of these libraries instead of sf for certain things.

Take for example calculating the length of linestrings on a geodesic. We can use the roxel dataset from {sfnetworks}.

data(roxel, package = "sfnetworks")

To illustrate, we can extract the geometry column and cast it as an rsgeo class object.

library(rsgeo)
geo <- roxel$geometry
rs <- as_rsgeo(geo)

We can then use the functions st_length() and length_haversine() respectively to compute the length of linestrings.

bench::mark(
  st_length(geo),
  length_haversine(rs),
1  check = FALSE
)
#> # A tibble: 2 × 6
#>   expression                min   median `itr/sec` mem_alloc `gc/sec`
#>   <bch:expr>           <bch:tm> <bch:tm>     <dbl> <bch:byt>    <dbl>
#> 1 st_length(geo)         6.34ms    6.8ms      140.    2.84MB     2.09
#> 2 length_haversine(rs) 457.01µs  515.3µs     1659.     8.8KB     0
1
check = FALSE because the distances are ever so slightly different likely due to floating point rounding or the radius of the earth that is used.

This is markedly faster when using rsgeo. We also do not have to extract the vector and work with it as its own object. Any vector can be included in a data frame, remember?

roxel |> 
  as_tibble() |> 
  mutate(
    geometry = as_rsgeo(geometry),
    length = length_haversine(geometry)
    ) |> 
  select(name, type, length, geometry)
#> # A tibble: 851 × 4
#>    name                  type        length
#>    <chr>                 <fct>        <dbl>
#>  1 Havixbecker Strasse   residential   28.8
#>  2 Pienersallee          secondary    108. 
#>  3 Schulte-Bernd-Strasse residential   54.3
#>  4 <NA>                  path         155. 
#>  5 Welsingheide          residential  209. 
#>  6 <NA>                  footway       63.0
#>  7 <NA>                  footway       42.2
#>  8 <NA>                  path          45.3
#>  9 <NA>                  track        348. 
#> 10 <NA>                  track        145. 
#> # ℹ 841 more rows
#> # ℹ 1 more variable: geometry <r_LINEST>

This same approach can work for other libraries such as geos.

library(geos)

roxel |> 
  as_tibble() |> 
  mutate(
    geometry = as_geos_geometry(geometry),
    length = geos_length(geometry)
    ) |> 
  select(name, type, length, geometry)
#> # A tibble: 851 × 4
#>    name                  type          length geometry                          
#>    <chr>                 <fct>          <dbl> <geos_geom>                       
#>  1 Havixbecker Strasse   residential 0.000331 <LINESTRING (7.53372 51.95556, 7.…
#>  2 Pienersallee          secondary   0.00101  <LINESTRING (7.53244 51.95422, 7.…
#>  3 Schulte-Bernd-Strasse residential 0.000505 <LINESTRING (7.53271 51.95209, 7.…
#>  4 <NA>                  path        0.00201  <LINESTRING [7.5382 51.945...7.54…
#>  5 Welsingheide          residential 0.00188  <LINESTRING (7.53767 51.9475, 7.5…
#>  6 <NA>                  footway     0.000585 <LINESTRING (7.54379 51.94733, 7.…
#>  7 <NA>                  footway     0.000408 <LINESTRING (7.54012 51.94478, 7.…
#>  8 <NA>                  path        0.000628 <LINESTRING (7.53822 51.94546, 7.…
#>  9 <NA>                  track       0.00430  <LINESTRING [7.5401 51.945...7.54…
#> 10 <NA>                  track       0.00162  <LINESTRING [7.5412 51.946...7.54…
#> # ℹ 841 more rows

If you plan on doing more than just one operation, it is best to convert to the desired geometry type only once and then use it in subsequent calls. Converting from one geometry type can take some time and add additional unwanted overhead if you’re doing it all the time.

roxy_geos <- roxel |> 
1  st_transform(25832) |>
2  as_tibble() |>
3  mutate(geometry = as_geos_geometry(geometry))
1
We project our dataset to use meters
2
We remove the sf class so we can modify the geometry column
3
We update the geometry from an sfc to a geos_geometry

With a geometry column that is a geos_geometry, you can use the functions from the geos package to perform your analyses. And, if doing larger scale analyses, it might be faster and more memory efficient!

roxy_geos |> 
  mutate(length = geos_length(geometry)) |> 
  group_by(type) |> 
  summarise(
    geometry = geos_unary_union(geos_make_collection(geometry)),
    avg_len = sum(length)
  ) 
#> # A tibble: 9 × 3
#>   type         geometry                                                  avg_len
#>   <fct>        <geos_geom>                                                 <dbl>
#> 1 cycleway     <MULTILINESTRING [399010 5756791...400105 5757567]>        2740. 
#> 2 footway      <MULTILINESTRING [398732 5755903...399949 5757266]>        4212. 
#> 3 path         <MULTILINESTRING [398473 5755558...399961 5757747]>        7525. 
#> 4 pedestrian   <LINESTRING (399313.41032 5756903.27258, 399269.10927 57…    44.8
#> 5 residential  <MULTILINESTRING [398511 5755623...400125 5757523]>       22495. 
#> 6 secondary    <MULTILINESTRING [398476 5755557...400104 5757548]>        3946. 
#> 7 service      <MULTILINESTRING [398470 5755810...399995 5757577]>        6600. 
#> 8 track        <MULTILINESTRING [399654 5755892...399975 5757362]>         974. 
#> 9 unclassified <MULTILINESTRING [398655 5755557...399971 5757726]>        1973.
roxel |> 
  mutate(length = st_length(geometry)) |> 
  group_by(type) |> 
  summarise(avg_len = sum(length)) 
#> Simple feature collection with 9 features and 2 fields
#> Geometry type: GEOMETRY
#> Dimension:     XY
#> Bounding box:  xmin: 7.522594 ymin: 51.94151 xmax: 7.546705 ymax: 51.9612
#> Geodetic CRS:  WGS 84
#> # A tibble: 9 × 3
#>   type         avg_len                                                  geometry
#>   <fct>            [m]                                            <GEOMETRY [°]>
#> 1 cycleway      2735.  MULTILINESTRING ((7.535912 51.95764, 7.536254 51.95772, …
#> 2 footway       4206.  MULTILINESTRING ((7.543791 51.94733, 7.54369 51.94686, 7…
#> 3 path          7513.  MULTILINESTRING ((7.523003 51.95298, 7.523524 51.95306),…
#> 4 pedestrian      44.7         LINESTRING (7.534819 51.95371, 7.534176 51.95364)
#> 5 residential  22457.  MULTILINESTRING ((7.533722 51.95556, 7.533461 51.95576),…
#> 6 secondary     3939.  MULTILINESTRING ((7.532442 51.95422, 7.53236 51.95377, 7…
#> 7 service       6589.  MULTILINESTRING ((7.532238 51.95388, 7.532069 51.9535, 7…
#> 8 track          972.  MULTILINESTRING ((7.540063 51.94468, 7.540338 51.94468, …
#> 9 unclassified  1968.  MULTILINESTRING ((7.534918 51.94681, 7.535121 51.94688),…

Continuing your R-spatial journey

With this, I encourage you to look at other geometry libraries available in the R ecosystem. Some of the notable ones are:

  • s2 for spherical geometry operations with google s2
  • geos bindings to the powerful libgeos C library
  • rsgeo bindings to the GeoRust geo-types and geo crates
  • wk for low level generic geometry interface with C and C++ APIs

Each library can convert to and from sf geometries as well.

Happy programming!

Reuse

Citation

BibTeX citation:
@online{parry2023,
  author = {Parry, Josiah},
  title = {R-Spatial Beyond Sf},
  date = {2023-09-08},
  url = {https://geocompx.org/post/2023/beyond-sf/},
  langid = {en}
}
For attribution, please cite this work as:
Parry, Josiah. 2023. “R-Spatial Beyond Sf.” September 8, 2023. https://geocompx.org/post/2023/beyond-sf/.